曲げモーメントとせん断力
曲げ応力
 実際の感覚をつかんでもらうために,、ここでは厚めの本を例にとって考えてみます。
実際の感覚をつかんでもらうために,、ここでは厚めの本を例にとって考えてみます。
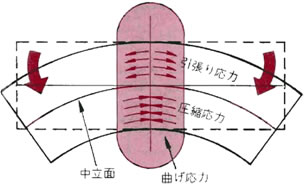
本(棒部材)を曲げた場合その力に対し曲げ応力が生じてきます。 曲げ応力のしくみは、右図のようになります。
本を曲げると、曲がった内側のほうは圧縮されて最初の長さより短くなろうとします。 外側は引張られて長くなろうとします。 ところが、一部分だけ圧縮も引張られもしない、最初の長さと同じ面があります。 これを中立面といいます。
この中立面を境にして上は引張り応力、下は圧縮応力が生じます。 これを総称して曲げ応力と言います。
棒部材の軸線に直角に荷重が作用する場合は曲げ応力と剪断力が同時にかかります。 一般にこのように横荷重を受ける棒のことを梁と呼びます。
 集中荷重を受ける片持ちばり
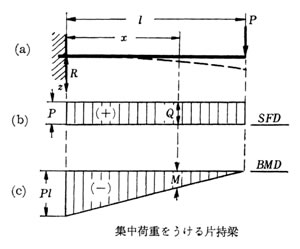
集中荷重を受ける片持ちばり
一端を固定し他端に横荷重 Pを採用する梁のことを片持ち梁といい1点に集中して作用する荷重のことを集中荷重という。
この場合横断面に作用する剪断力Qはどの位置に置いても一定である。
軸線に沿ってのせん断荷重分布を示したのが (b) 図でこれを剪断力図という。 これに対して曲げモーメント分布を示した物が (c)の曲げモーメント図である。
固定端から x だけ離れた横断面に作用する曲げモーメントは M = P(l-x) であり 最大曲げモーメントは、固定端に発生し M max = Pl である。
 等分布荷重を受ける片持ちばり
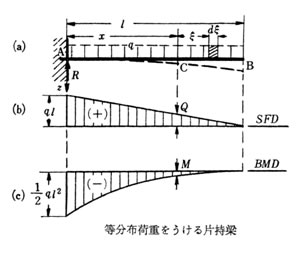
等分布荷重を受ける片持ちばり
梁に横荷重が一様に分布しているものを等分布荷重と言いい、単位長さあたりの荷重の大きさを q で表せばCB間の荷重の合計は q (l-x) となり断面 Cに作用する剪断力は Q = q (l-x) となる。
ここでも 最大曲げモーメントは 固定端にあり 、Q max = ql^2 / 2 で表される。
集中荷重では、ある1点に重さ100Kgが、かかればPは100kgですが、分布荷重の場合は単位あたりの重量ですので1000mmの長さの梁であれば自重100kgを1000で割って0.1Kg/mmとなります。 梁の長さをCmで計算していれば1Kg/cmです。
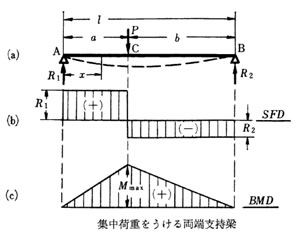 集中荷重を受ける両端支持梁
集中荷重を受ける両端支持梁
両端A ,B が支持された梁を両端支持ばりといい、AB間の距離 l をスパンという。
はり上の1点 Cに集中荷重 P が作用するとR1, R2に反力が生じ R1, R2にははりに対し外力が作用し P, R1, R2の間には力およびモーメントの釣り合いができる。 P = R1 + R2で表される。
AC間の任意断面に作用する剪断力、曲げモーメントを考えるとき このはりをC点にて固定された片持ちばりと考える。
Q = (b/l)P 、 M = (b/l)x Pで 計算できる。 同様にCB間も Q = (a/l)P 、M = (a/l)(l-x)Pとなる。
断面2次モーメント
断面の形状によってのみ決まる。
曲げられる方向により変化する。
中立軸の位置から一番 遠いところに最大の応力が発生するので、そこにどれだけ面積を多く配置できるかによりその大きさがきまる。
それぞれ形状により断面2次モーメントの計算式 (excel dataはこちら)があります
右の長方形では bh^3/12 となります。 同じ断面形状、断面積であっても曲げられる方向に対する中立軸の位置で大きく異なります。
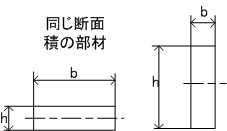 右の例でいけばhの値が3乗されるので たとえば 10 x 50の板であれば 左は4166 右は104166となる。
右の例でいけばhの値が3乗されるので たとえば 10 x 50の板であれば 左は4166 右は104166となる。
ここで気をつけたいのは板材は 曲げられる方向に対して縦に配置する事が効率的であると言うような単純に解釈しないことです。
H形の部材で考えてみましょう。 A,Bは同じ断面です。
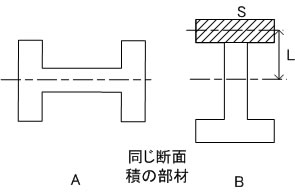 板材の例からするとAの方が断面2次モーメントは大きくなりそうですが、実際にはBの方が多くなります。 これは中立軸からの距離が大きく関係してきます。
板材の例からするとAの方が断面2次モーメントは大きくなりそうですが、実際にはBの方が多くなります。 これは中立軸からの距離が大きく関係してきます。
断面2次モーメントはB部材にハッチングした部分のように単純形状の断面2次モーメントの集合体として計算できます。
従いハッチングの部分の断面2次モーメントは単純板の計算式を使い計算できます。
下側にも同じ断面があるのでこの断面2次モーメントの2倍プラス立てに入っている物を足せば合計がひとまずでます。
次に各断面の中立軸と全体の中立軸の距離 Bの例で行けばLを出します。
このLの値が非常に大きく影響してハッチングの面積 X Lの2乗が足されます。
実際のH鋼の 断面2次モーメントを みて確認してみましょう。
一桁以上 違うのが確認できたと思います。
このH鋼は強度的に非常に効率のよい形状をしているため 建設鋼材としてもっとも使用される理由の一つです。
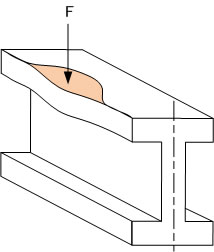 しかし、この中立軸からの距離だけを取ることで計算上は十分な強度をとれていると思うのは早計で もう一つ考慮しておく必要があります。
しかし、この中立軸からの距離だけを取ることで計算上は十分な強度をとれていると思うのは早計で もう一つ考慮しておく必要があります。
全体断面の弱い部分に局部的、1点集中の力が加わらないことが重要です。 もし 1点に荷重が集中してしまう場合は、断面2次モーメントと言う概念で計算してはいけません。 あくまでも荷重がかかる特定の狭い範囲だけの部位で計算しなければなりません。
部材の形状をどのようにすれば強度的に効率的かを考慮することは非常に重要です。
シュミレーションでは、結果だけしか計算してくれません。どのように対策するかは設計者のスキルで決まります。
断面係数
断面2次モーメントを中立軸から表面までの距離で割ったもの。
曲げモーメントが働くときの最大応力を計算するのに使用される。
断面係数が大きいほど最大応力は小さくなる。
σ=最大応力、 M =曲げモーメント、 Z = 断面係数とすると 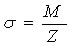 となる。
となる。
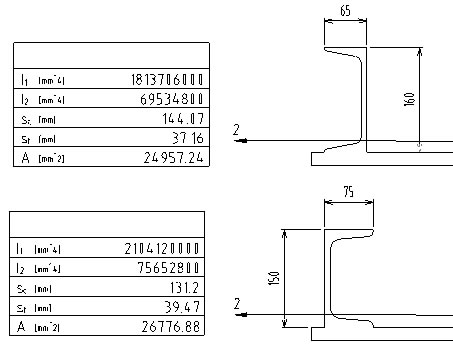
恐るべし中国形鋼
中国のチャンネルの断面は日本のものと相当違うのをご存じでしょうか? 私は今まで知りませんでした。
しかも、160と言う高さの中国規格のチャンネルは、日本の150のチャンネルよりも弱い(断面2次モーメントが小さい)のです。
はじめ、また、この図面はいい加減なチャンネルの断面を書いているなーと、思っていたのですが、調べてみると現物もこのような形になっているとのこと、チャンネルの先端がRのまま終わっている。直線部分がないのです。
これでは、一番、強度に重要な外皮部分に面積がなくなってしまい強度が確保できなくなります。
中国(海外)の形鋼を使用するときは十分に気を付けたいものです。
日本の図面を使い中国で作成する場合に材料は現地調達が基本ですから、その場合 通常 外形寸法で置き換えますからよほど注意深く見ているところでないと見過ごしてしまうのでしょうね。
うーん 恐るべし 上が中国の形鋼です。