長柱の座屈
圧縮荷重をうける棒を柱といい、柱が軸方向に圧縮される場合に荷重の合力が端面の図心を通って軸線方向に作用すれば、横断面には圧縮応力が一様に分布し、柱は軸方向に縮むが彎曲しないはずです。
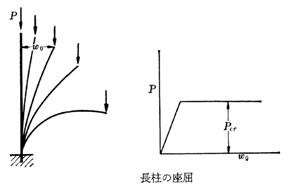
しかし実際には柱は彎曲し、柱が細長くなるにつれて彎曲し易くなる。
これは最初から柱が僅かに彎曲しているか、あるいは柱の材質が均質でないことに原因し、そのような場合には軸線に一致して端面に荷重を加えても、偏心荷重が作用する場合と同様に、各横断面には曲げモーメントが作用することになります。
もしも柱に偏心荷重が作用すれば、右図のように、荷重が増すにつれてひずみは次第に大きくなり、柱に作用する曲げモーメントは荷重およびひずみに比例して増大し、ある荷重 Pcr に達すれば、荷重を増さなくてもひずみのみが大きくなり、ついには柱が破壊する。
このような現象を座屈といい、 このときの荷重 Pcr を座屈荷重という。
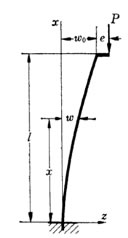
いま一端を固定した長さ乙の柱の端面に,図102のように図心からθだけ離れた点に圧縮荷重 P を加えることにする。
通常の考え方によれば、柱に作用する曲げモーメントは (-Pe) であるけれども固定端から x だけ離れた点は ωだけひずんでいるから厳密にはこの点に作用する曲げモーメントは M = -P(ω0 + e - ω) となる。 座屈荷重 Pcrは 柱の支持の仕方により 以下の計算式で表される。
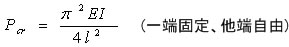
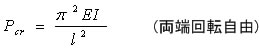
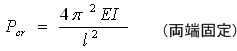
長柱の座屈に関する以上の式はオイラーの公式と呼ばれる。
理想的な座屈においては、P = Pcr になるまでは柱は全くひずまないから、座屈直前に柱に生じている圧縮応力を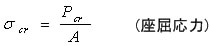
座屈応力という。
これに オイラーの式を代入して座屈応力をもとめると次式になる。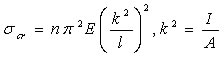 
このとき A= 断面積、 I = 断面2次モーメント、 k = 最小断面2次半径とする。
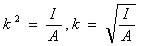となる。
ここで k を断面二次半径として l/k を柱の細長比といい、材料が同じならば、細長比が小さいほど座屈応力は大きい、 オイラーの公式は座屈荷重に達するまでに柱に生ずる応力は弾性限度内にあると考えて導いたものである。
しかし柱が短かいならば,座屈荷重に達する前に圧縮応力σc = P/A が弾性限度を越えるようになる。
このような短かい柱に対してはオイラーの公式は適用できない。
座屈応力を材料の降伏点に等しくおけばオイラーの公式が適用できる柱の長さの限界は
、
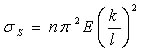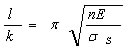で求められる。