回転体
回転運動における仕事とは 回転物体にトルクが作用して ある角度回転した場合 トル クの大きさと回転角の積で表わされる。
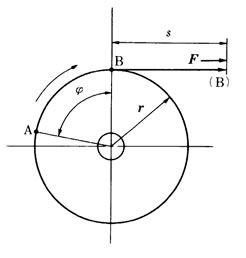直線運動の場合と比較して説明すると 右図に示すように 半径γのベルトプー・リの軸 にトルク T が作用した状態で 軸が角度ψだけ回転し 外周上の点Aが点Bへ距離 s だけ移動したとする。
この場合距離 sは s = rψ また 外周上に作用する力 F は F = T/r であるから仮想的に外周上にロープを巻いて これを 力 F で S だけ引いた場合を考えれぼ 仕事は ROTATE7 すなわち E = Tψ したがって 回転運動においては仕事は トルクと回転角の積となることがわかる。
次に回転体の運動エネルギであるが 物体が運動しているとき エネルギ保存の法則により運動エネルギーをもつが これは運動の形態に関係なく 回転運動の場合にも回転運動のエネルギーを持っている。
直線運動と回転運動の関係
力 F 、質量 m、加速度α、トルク T、 速度 v 、角速度 ω、 直線移動距離 S、 移動回転角度 ψ、 慣性モーメント I
t 時間とすると
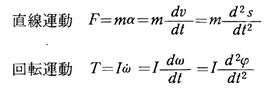
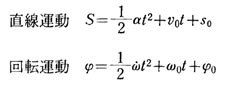
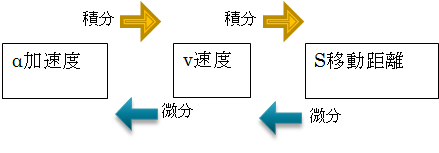
運動エネルギーは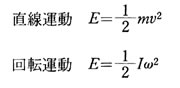
となる。
それぞれv0,ω0初期速度、s0,ψ0初期位置 とする。
| 直線運動と回転運動の比較 | |||
| 直 線 | 回 転 運 動 | ||
| 力, [kgf」 |
F (N) |
トルク,[kgf・m] | T (N・m) |
| 質 量 [kgf・s2/m] |
m (kg) | 慣性モーメント, [kgf・s2m] | I (kg・m2) |
| 加速度, m/s2 | α | 角加速度 rad/s2 | ω |
| 速 度, m/s | v [m/min] | 角速度,rad/s | ω,[n」 [rpm] |
| 変位(移動距離),s m | 角変位(回転角),ψ rad [度(°)] | ||
| 時間 sec t [min] | |||
| 運動エネルギ(仕事) E [kgf・m](N・m)(J) |
|||
トルク T、ワット P、 慣性モーメント Aの関係式
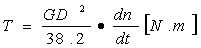
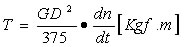
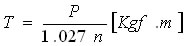
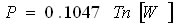
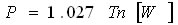
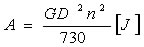
1馬力 = 0.7457 Kw