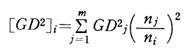等価GD2計算法
回転体の保有する運動エネルギは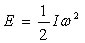 
実際の設計においては、力学的な角速度ωよりも軸の回転数 n/rpmを用いることが便 利であり、また一般に行われている。
式を利用しやすいように、回転数 n/rpm を用いて表わすと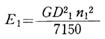
分母の値は、各地点の重力の加速度 g の値により異なるが、ここでは慣例として一般に用いられる7150とした。
上式よりわかるように、運動エネルギはGD2に比例し、回転数の2乗に比例するので、 機械装置が大型化するほど、また高速化するほどエネルギが大きくなり制御に注意を要する。
連動する回転体の等価GD2
機械装置には、歯車列やプーリなど回転運動装置や、その他回転体を多数連動する場合が多い。
こうした連動装置を用いて、加速や減速、位置などの制御を行う場合、一般にモータ軸が制御軸に選ばれている。
これは駆動は当然としても、制動の場合もブレーキ装置の取付けを、なるべく高速軸で行ったほうが、フレーキ容量を小さくすることができるためである。
したがって、連動装置のGD2は、モータ軸換算の等価GD2として求めることが多い。
もちろん、増速軸がある場合や空間的な設計処理の都合などで、他の軸が制御軸となる場合は、その特定の制御軸に関して換算されたGD2が求められる。
このGD2の換算法は、回転数およびGD2の異なる連動回転運動体の保有するエネルギを考え、これに対してある回転数で 回転する特定軸が、これら連動体のもつエネルギの総和と等しいエネルギをもつには、どれだけのGD2がこの軸に関してあればよいかと考えれぼよい。
右図は、モー‐タによって駆動される歯車列を示したものである。
モータ軸を軸1、歯車軸を軸2とし、回転数を n1, n2 rpmとする。
軸1に関するモータとピニオソおよび軸1のGD2の和をGD2_1,軸2に関するギヤと軸2 GD2の和をGD2_2とすれば、各軸に属する回転運動のエネルギE1,E2 は、それぞれ
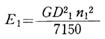
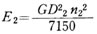いま、軸1(回転数 n1)を制御軸として、軸2(回転数n2)のGD2_2を軸1に関する等価GD2_1に換算すると、エネルギ保存の法則により、これらのエネルギは等しくなければならないので、 
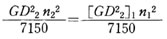展開して
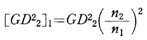
上式は、運動エネルギを等しいと置いて換算することにより、求められたものであって、軸が連動さえしていれば軸回転数比が定まるので軸1と軸2は必ずしも隣り合っている必要はない。
整理すると
na : 軸 aの回転数(rpm) ni : 任意の換算軸 i の回転数(rpm)
GD2_a : 軸 aに属するGD2 [GD2_a]i : GD2_aを軸に換算した等価GD2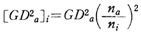 
換算したいGD2に その軸と換算する特定の軸との回転数比 の2乗をかければ、 等価GD2が得られることになる
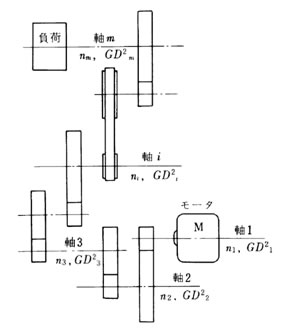
この換算法を一般化して考えてみる。
右図に示すように、多数の回転体が連動する場合を考え、モータ軸1に関する等価GD2を計算することにする。
各軸の回転数 : n1,n2 ...・・ 各軸のGD2 : GD2_1 GD2_2・・・... とすると、モータ軸1に関する等価GD2は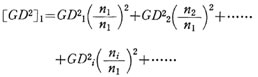
また任意の軸 i を特定の制御軸として、軸 i に関する装置の等価GD2を計算する場合は、任意の整数を j として一般式で表わすと
