力学

力のモーメント

力のモーメントについて

物体を廻そうとする力のことをモーメントと言う。

モーメント = 長さ x そ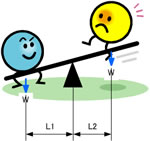の先端に働く直角方向の力 です。

左の図では 長さ L1 X 力 W > L2 X 力 W となります。

Wが同じ重さであるとすれば 中心からの距離 L1 > L2 なので 左の方が モーメントが大きくなり 左に傾くこととなります。

小学生でならった やじろべえ、てこの原理と同じです。

左辺と右辺が同じ値になったときにはつり合うことになります。

ここで一つ気をつけなければいけない点があります。

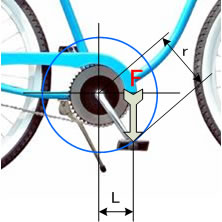L の距離の測り方に注意してください。

わかりやすい例として 自転車のペダルがあります。

ペダルをこぐためには 通常 下側に 力を加えます。

そうするとペダルを回転させようとする力は L X F になります。

r X Fではない点に注意してください。

その証拠に ペダルが 最下点、最上点にきたときに幾ら力を真下にかけても回転力は発生しません。

モーメントを計算する上での長さとは 作用する力に直角線を引きと回転中心で交わる点との距離です。

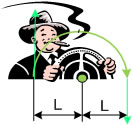左の車のハンドルを廻すときのように 力の大きさが同じで 方向が反対で廻そうとする力を 偶力のモーメントと言います。

この偶力は安定した力の状態です。 実際の世界で物を廻そうとしたときに片側だけに力をかけようとした場合 長さ L を 2倍にすれば 偶力と同じMOMENT3モーメントが発生します。

ただし、理論上ではです。 車のタイヤを交換するための十字レンチをご存じでしょうか? これです。 メンテキットに入っている片側だけに力をかける物に比べて 格段に ナットをはずしやすいです。

なぜでしょうか? それは 片側だけに力が加わったときに回転力だけでなく レンチを曲げようとするなど 複雑な余分な力に分散してしまうからです。

トルクとは

直線運動における力に相当するものが 回転運動におけるトルクです。 考え方は 力のモーメントと変わりません。 参考に 直線運動と回転運動の対比表を 示します。

直線運動			回転運動
力	F	N	トルク	T	N.m
質量	M	kg	慣性モーメント	J	kg..m2
加速度	α	m/s2	角加速度	αθ	rad/s2
速度	ν	m/s	角速度	ω	rad/s
距離	s	m	角度	θ	rad